Przy tej okazji należy wspomnieć o jeszcze jednej rzeczy. Otóż, w myśl Ogólnej Teorii Względności siły grawitacji i bezwładności są równoważne, nie da się ich odróżnić. To by znaczyło, że podczas obliczania pozycji domów zamiast szerokości geograficznej należałoby brać kąt nachylenia lokalnego pionu (wypadkowej siły grawitacji i sił bezwładności) do płaszczyzny równika. Na szczęście, w praktyce różnice są zaniedbywalne.
Wyróżniamy cztery punkty kardynalne podziału na domy: Zenit (Z), Nadir (Nd), Wschód (E) i Zachód (W). W myśl mojej koncepcji, wszystkie te punkty oddziaływałyby na każdy obiekt na Sferze Niebieskiej, czyli innymi słowy każde ciało niebieskie odczuwałoby wpływ wszystkich domów. Brzmi to bardzo dziwnie, więc zaraz dorzucam: wszystkich, ale z różną siłą. Ta siła szybko malałaby wraz z odległością kątową od punktu kardynalnego, czyli w ten sposób oddziaływanie Zenitu przeważałoby na południku miejscowym (Medium Coeli, część koła wielkiego przebiegająca nad horyzontem), oddziaływanie Wschodu na wschodniej połówce horyzontu (ascendent), Nadiru po przeciwnej stronie do Medium Coeli (Imum Coeli, część koła wielkiego będąca pod horyzontem) i Zachodu na zachodniej połówce horyzontu (descendent). Punkty leżące na horyzoncie dokładnie na południu (S) i północy (N) byłyby wyróżnione o tyle, że znajdowałyby się w odległości 90° od wszystkich punktów kardynalnych, czyli jednakowo odczuwałyby wpływ wszystkich domów, a więc efektywnie wpływ domów malałby do zera. Na razie zajmuję się wierzchołkami domów narożnych (I, IV, VII i X), o pozostałych domach wspomnę później.
Ktoś może zapytać: a jak w takim razie wyglądałaby ta "siła" oddziaływania ? To powinno być rozstrzygnięte doświadczalnie (najlepiej przy pomocy badań statystycznych), ale na początek proponuję następującą zależność:
I(d) = A * exp [ B * cos(d) ]
gdzie d jest odległością kątową od punktu kardynalnego (rzeczywistą, mierzoną na sferze a nie na ekliptyce!), A jest stałą normalizacyjną (nie mającą znaczenia przy porównywaniu względnej siły oddziaływania), zaś B jest parametrem, który trzeba wyznaczyć. Stała B określałaby, jak ostre są granice między domami: duża stała oznaczałaby ostre, wyraźne granice i na odwrót (np. B=0 oznaczałoby równy wpływ wszystkich domów).
W ten sposób wyznaczylibyśmy wierzchołki domów narożnych, teraz powstaje pytanie: a co z innymi? Widzę przynajmniej dwie możliwości:
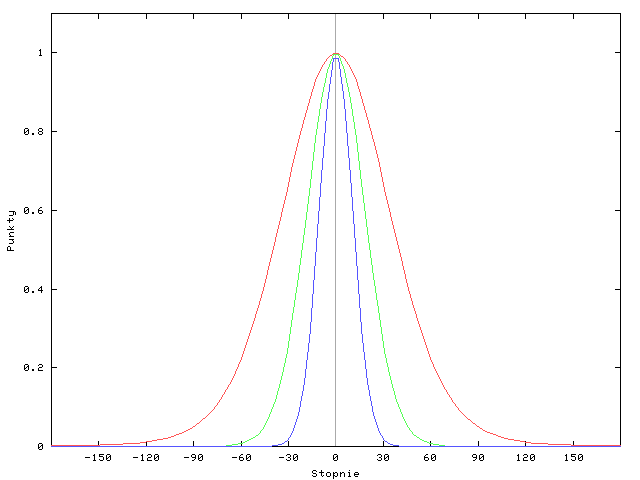
Zależność krzywej intensywności oddziaływania domu od stałej B jest pokazany na poniższym rysunku:

Krzywa czerwona odpowiada najmniejszej wartości stałej B (tu akurat równej 3), zielona pośredniej (10) a niebieska największej (30). Z kolei efekt dominacji oddziaływania konkretnego domu nad oddziaływaniem pozostałych widać na następnym rysunku:

Tu przyjąłem stałą B równą 10. Krzywe zielona, czerwona i ciemnoniebieska pokazują siłę oddziaływania poszczególnych domów podzieloną przez zsumowany efekt oddziaływania wszystkich domów, zaś krzywa jasnoniebieska pokazuje sumę efektów oddziaływań wszystkich 12 domów podzieloną przez wartość w punkcie 0. Widać, że każdy kolejny dom dominowałby na obszarze o szerokości 30° a suma wszystkich oddziaływań byłaby prawie stała, mniej niż 2 razy większa niż maksimum oddziaływania każdego z domów.
Kolejna kwestia: zanik domów na biegunach geograficznych. Z tym będzie nieco trudniej, choć proponuję następujący model matematyczny (mała zabawa wektorami):
Oznaczmy wektor normalny (prostopadły) do powierzchni Ziemi w danym miejscu przez n. Łatwo zauważyć, że Zenit jest punktem przecięcia wektora n ze Sferą Niebieską, zaś Nadir jest punktem jej przecięcia z wektorem -n. Oznaczmy wektor (a właściwie pseudowektor) prędkości kątowej Ziemi przez w (ściślej, powinno być małe omega, ale to dopiero będzie w PostScriptowej wersji tego tekstu). Łatwo zauważyć, że punkt Wschodu leży na przecięciu Sfery Niebieskiej z wektorem w×n ("×" oznacza iloczyn wektorowy) a punkt Zachodu na przecięciu Sfery Niebieskiej z wektorem przeciwnym (nazwijmy te wektory "wektorem ascendentu a i "wektorem descendentu" d). Kolejne spostrzeżenie: na biegunach te iloczyny wektorowe wynoszą zero, gdyż tam wektory normalne są równoległe do wektora prędkości kątowej Ziemi, czyli mamy od razu zanikanie ascendentu i descendentu ! Powstaje pytanie, co zrobić z MC i IC? Aby te rozważania miały sens, ich wpływ powinien zanikać proporcjonalnie do zaniku wpływu Asc. i Dsc. Proponuję następujące rozwiązanie: ponieważ domy są związane z obrotem Ziemi wokół swej osi a na biegunach liniowa prędkość obrotu jest zerowa (bo jest proporcjonalna do cos(f), gdzie f jest szerokością geograficzną), podobnie jest z kołami zataczanymi przez Zenit i Nadir na Sferze Niebieskiej, więc ich "siła" również byłaby proporcjonalna do cos(f). Jeśli to wyrazić za pomocą wektorów, to "wektor MC" m wyrażałby się wzorem n*|w×n|/|n|, gdzie |x| jest długością wektora x ("wektor IC" i różniłby się tylko zwrotem). Aby usunąć asymetrię między wzorami na wektory a i d a m i i należałoby je wszystkie pomnożyć przez |n| :
a=|n|*w×n , d=-|n|*w×n , m=|w×n|*n , i=-|w×n|*n
I jeszcze dwie uwagi, dlaczego tak się upieram przy zależności od cos(d) zamiast po prostu od d:
Osobną sprawą jest kwestia aspektów do Asc, Dsc, MC i IC. Jeśli przyjąć moją koncepcję, w myśl której aspekty zależą od odległości kątowych na sferze niebieskiej (a nie na ekliptyce), to mogłyby być pewne problemy z koniunkcjami i opozycjami do Punktów Kardynalnych - byłyby możliwe tylko na niektórych szerokościach geograficznych; jeśli brać pod uwagę obiekty na ekliptyce, to w grę wchodziłyby obszary równikowe oraz położone w pobliżu zwrotników. Ale przecież w myśl rozpatrywanej koncepcji np. Ascendent nie byłby punktem tylko połówką horyzontu, stąd raczej trzeba wypracować odmienną koncepcję aspektów, niż dla obiektów działających punktowo (np. planety czy Światła). Jedynym rozwiązaniem, jakie mi w tej chwili przychodzi do głowy, byłoby branie odległości kątowych na I Wertykale. Konsekwencje byłyby następujące:
To dotyczy strefy umiarkowanej, ale powstaje pytanie: a co na równiku i, ogolnie rzecz biorąc, pomiędzy zwrotnikami? Tam w ciągu roku są w zasadzie dwie pory cieplejsze i dwie chłodniejsze, tak więc "wiosenny" Baran nie ma sensu. Nasuwa się wniosek, że na równiku Zodiak tropikalny nie powinien mieć żadnego znaczenia.
Zastanówmy się, jak opisać "natężenie wpływu Zodiaku tropikalnego". Potrzebujemy funkcji, która na biegunie północnym będzie miała wartość największą (np. 1), powinna maleć wraz z malejącą szerokością geograficzną, na równiku będzie równa zero, zaś jej przebieg na półkuli południowej będzie "antysymetryczny" (tzn. f(-x)=-f(x)) do półkuli północnej. Jeśli ograniczyć sie do funkcji trygonometrycznych, powyższe warunki spełniają wyłącznie funkcje postaci sin(2n+1) f, gdzie f to szerokość geograficzna a n to jakaś liczba naturalna; mogłaby być też jakaś kombinacja tych funkcji (np. 0.5(sin(f) + sin9999(f))). Oczywiście, najprostszym rozwiązaniem jest zwykły sinus (czyli sin(f)).
Tu przypomnę, że w myśl mojej hipotezy z domami powinno być na odwrót: największe znaczenie powinny mieć na równiku a powinny zanikać na biegunach - postulowałem opisanie ich "natężenia" przy pomocy funkcji cos(f), a jeszcze lepiej cos2(f) (ma bardziej "gładkie" zachowanie na biegunach).
Wszystko ładnie, ale np. w astrologii hinduskiej posługują się Zodiakiem gwiazdowym a nie tropikalnym. Przez dłuższy czas nie wiedziałem, "co z tym fantem zrobić", ale w końcu wpadłem na następujący pomysł: Zodiak gwiazdowy jest niejako drugą składową Zodiaku, niezależną od szerokości geograficznej!
Pomyślmy: przez Indie przechodzi równik, a więc tam Zodiak tropikalny miałby (w myśl mojej hipotezy) minimalne znaczenie. Europa jest daleko od równika i u nas (według danych tradycyjnych) obowiązuje Zodiak gwiazdowy. Da się to pogodzić w sposob następujacy: u nas Zodiak tropikalny jest wyraźnie silniejszy od gwiazdowego, u nich Zodiak tropikalny jest bardzo słaby i dlatego "odczuwają" głównie gwiazdowy.
Jesli wyrazić to w jezyku funkcji: powiedzmy, że względna "siła" Zodiaku tropikalnego na biegunie północnym jest równa 1. Wtedy np. w Krakowie (szerokość geograficzna 50°) byłaby równa sin(50°) = ok. 0.77. W Indiach byłaby w granicach ok. +/- 0.2 ("-" dla półkuli południowej!). W takim razie względna "siła" Zodiaku gwiazdowego powinna leżeć gdzies pomiędzy, np. być równa 0.4. Interpretacja znaków w Zodiaku gwiazdowym i jego punkt poczatkowy to osobne problemy - np. moim zdaniem nie powinno się automatycznie przenosić europejskiej interpretacji znaków Zodiaku, mogą (powinny?) wystepować spore różnice.
Prawdopodobnie pełny opis Zodiaku powinien być bardziej skomplikowany, gdyż powinien uwzględniać fakt, że wprawdzie na biegunach różnice między porami roku są największe (dzień i noc polarna) a na równiku najmniejsze, ale jeśli chodzi o nasłonecznienie (a co za tym idzie, pory roku), to Ziemię można podzielić na trzy typy stref:
Weźmy choćby sytuację na równiku. Ponieważ tam w ciagu roku wystepują dwie pory cieplejsze i dwie chłodniejsze (przy czym w miarę zbliżania się do zwrotników różnice między obydwiema porami np. cieplejszymi stają się coraz większe), więc to dawałoby w efekcie trzecią składową, występującą tylko w obszarze równikowym - nazwijmy ją "kwadrupolową" (dwa maksima i dwa minima). "Zwykły" Zodiak tropikalny byłby "dipolowy" (jedno maksimum i jedno minimum).
W tej sytuacji proponuję następujące rozwiązanie (tu mnie zainspirowały całki po trajektoriach znane z mechaniki kwantowej): wprowadzić funkcję siły I(d) (prawdopodobnie byłaby to ta sama funkcja, co w przypadku domów) i wtedy liczyłyby się obydwa midpunkty, ale z różną siłą: jeden oddziaływałby z siłą I(d1) a drugi z siłą I(d2) gdzie d1 i d2 oznaczają odległości między obiektami brane po jednym i po drugim łuku. Wtedy na pierwszy midpunkt przypadałby ułamek I(d1)/[I(d1)+I(d2)] sumarycznego oddziaływania a na drugi I(d2)/[I(d1)+I(d2)]. Podobnie byłoby dla horoskopów kontaktowych n osób - tyle, że byłaby większa ilość składników sumy. Wszystko zależałoby od kształtu zależności I(d) - jeśli byłaby bardzo stroma (szybko malejąca wraz ze wzrostem d) to mielibyśmy ostrzejsze granice (tzn. liczyłyby się praktycznie wyłącznie bliższe midpunkty) i na odwrót.
Powyższe rozważania stosują się do astrologii tradycyjnej, ograniczonej do ekliptyki. Jeśli rozszerzyć to na sferę, to zamiast dwóch punktów otrzymamy koło wielkie i wtedy mielibyśmy nieskończenie wiele punktów, przy czym najsilniejsze byłyby punkty wokół połowy najkrótszego łuku między obydwoma obiektami a suma zostałaby zastąpiona przez całkę po tym kole wielkim. Na razie nie byłoby to specjalnie użyteczne w praktyce astrologicznej, ale w przyszłości - kto wie ?
Czy ma to jakieś konsekwencje dla punktów arabskich? Ma, gdyż ich wyznaczanie zależy od tego, czy osoba się urodziła w dzień czy w nocy, stąd wątpliwości w wypadku, gdy Słońce znajduje się w pobliżu horyzontu. I znów, aby uniknąć nieciągłości, proponuję uznać, że liczą się obydwa punkty: dzienny oddziaływałby z siłą obliczoną dla odległości Słońca od Zenitu a nocny oddziaływałby z siłą obliczoną dla odległości od Nadiru. Jeśli wysokość Słońca oznaczyć przez h (h dodatnie oznacza położenie nad horyzontem i na odwrót) to punkt dzienny oddziaływałby z siłą I(90°-h) a nocny z siłą I(90°+h) - w dzień silniejszy byłby dzienny, w noc nocny a przy wschodzie lub zachodzie Słońca obydwa oddziaływałyby z jednakową siłą. Sytuacja by się skomplikowała, gdyby przyjąć moją koncepcję domów - prawdę mówiąc, na razie nie znalazłem satysfakcjonującego rozwiązania. Prawdopodobnie należałoby jakoś dodawać odpowiedni łuk do punktu Wschodu albo zrzutować wszystko na Pierwszy Wertykał. Albo w ten sposób: zatoczyć okrąg o promieniu danego łuku wokół punktu Wschodu i uznać któryś kierunek za bardziej zgodny z urodzeniami dziennymi a przeciwny za zgodny z urodzeniami nocnymi - wtedy znów, jak w przypadku midpunktów, otrzymalibyśmy koło zamiast dwóch punktów, przy czym tym razem prawie zawsze byłoby to koło małe.