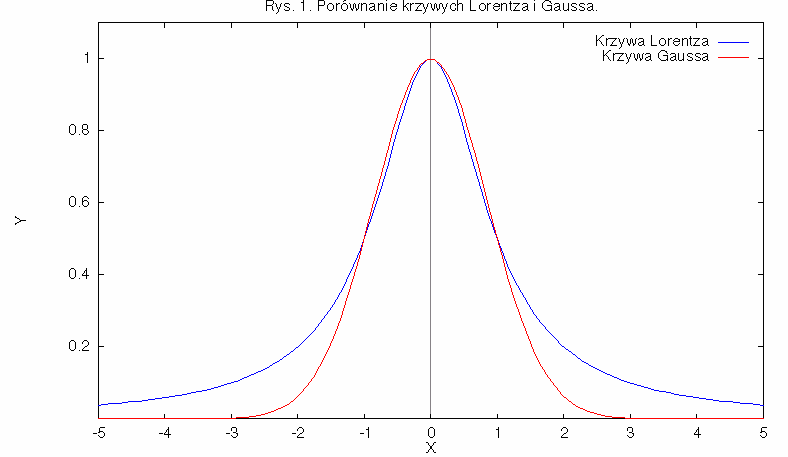
Now we have a good time to do mathematical description of these phenomena. Resonances may be described using intensity curves. Their shape is usually a Lorentz curve described by equation
y = a / ( 1 + (x/b)^2 )
where a and b describe intensity and width of the curve. Another common distribution is the Gaussian one described by equation
y = a * exp ( -1/2 (x/b)^2 )
but it is applied usually when describing random phenomena like errors distribution. If compared to the Lorentz curve its maximum is flatter but it goes to zero much faster for arguments distant from zero. Both distributions are shown at Fig. 1 where they are normalised in such a way that for x=0 y=1 and for x=+/-1 y=0.5 (the same intensity and the same width at half of intensity).

Now let us think about the nature of this resonance. The situation is a bit complicated: we have not only intensity but also aspects are regarded as good, bad or neutral (I think good means less difficulties and bad more, the best situation is when there is more or less equilibrium between them - too much good aspects makes person to be lazy, he (or she) does not achieve anything significant in life or breaks down in case of difficulties). Of course, the strongest is the 1:1 resonance (conjunction) and it is neutral (the result depends on the nature of planets). 1:2 resonance (opposition) gives negative effects, 1:3 (trine) positive, 1:4 (or: double 1:2 or square) gives weaker effects than 1:2 but more negative etc. It seems that:
Before we have a theory fully describing aspects I suggest following solution:
Now I must ask a question: do aspect really depend on differences of ecliptic longitudes? Ecliptic is the plane of Earth's orbit around the Sun only. Maybe they do not depend on differences of ecliptic longitudes but real angular distances on the Celestial Sphere? For the Sun, the Moon and planets up to Neptune it would be almost the same - they are never far from the ecliptic (up to 5° for the Moon). There would be one important difference: in fact, no exact conjunctions and oppositions (even if ecliptic longitudes were the same there would be some difference in latitudes). Pluto would be in a different situation - its latitude can reach +/- 17° so in most cases (north or south latitudes greater than 10°) there would be no conjunctions and oppositions. Even worse with stars - only stars near ecliptic would be significant (conjunction!), e.g. Sirius (b=-39.6°) would be not significant. But there would be no problems with objects near ecliptic poles (no ecliptic longitude) - they would be in square to objects on ecliptic. There would be problems with traditional adding aspects - two exact sextiles might not to give an exact trine (it would be O.K. if they were coplanar with Earth).
I must ask some questions: does ecliptic have any meening apart from that planets' orbits lie in its neighbourhood? Maybe we should take right ascensions instead of ecliptic longitudes? And why right ascensions and not galactic longitudes? What is the meaning (if any) of the Spring Equinox Point? What are Zodiac signs, what are their real boundaries, what is their influence's distribution? Some people claim that Zodiac are some energetic zones around Earth or that signs have some magnetic forces. So maybe we should look at magnetic poles instead of geographic ones? And what is the energy of these zones - connected with electromagnetic interactions? Strong? Weak? Gravitational? Electroweak? Maybe with so-called fivth force? We can exclude direct gravitational attraction (furniture's influence would be greater and, for example, Mercury's influence would be 6 mln. times lower than the Sun's one). I think we should not to talk about energies - we simply do not know how it works and some astrologers' speculations make existing chaos to be greater only. The right answer could be given by scientific research only.
At Fig. 2 there is an example how can the interaction curves for houses look like. I defined a variable alpha = (n-1+x/d) * 30° where n denotes the house number, x is the distance from the cusp and d is the diameter of the house. Alpha shows the house and the position in the house where the body is. For Asc alpha=0, for IC alpha=90° etc. (for the cusp of n-th house alpha = (n-1) * 30°). More precisely, this formula is an approximation, exact calculation of alpha is complicated and depends on the system of the houses.
Solid line denotes curves for odd houses, dotted line denotes curves for the even ones and the dashed-dotted line shows the sum of them. For the odd houses I took the function 1.5 + sin (6 alpha) + 0.5 cos (12 alpha), for the even ones the same function but with 30° shift in phase. Why such functions? First of all, they are a simple combination of trigonometric functions; moreover, they are almost constant entire the house; last but not least, out of the house they gradually decrease and they are zero in the half of the next (or previous) house. They are symmetric to the center of the house, the influence of the house starts in the half of the previous one and ends in the half of the next one. The sum is the greatest in the cusp and the lowest in the center of the house. In other words: in the middle the power of an object would be the weakest but the influence of the house would be the strongest. In the border between two houses the power of an object would be the strongest but it would be equal influence of both houses. But there is another question: what would be implications for the estimate of the strength of the planet?
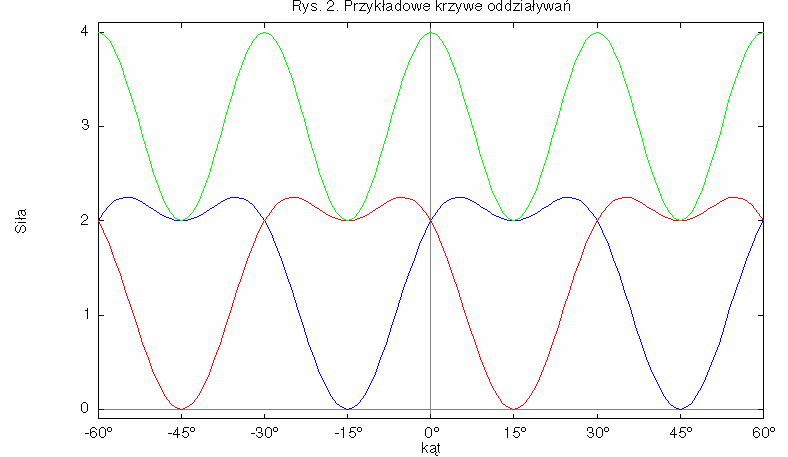
Of course, it can look different, it does not need to be symmetric, the influence of the next house can start in the last 5° of the house etc. - no problem, each integrable periodic function can be expanded using Fourier series (an trigonometric expansion, usually infinite).
I think that the Fourier expansion can be used as a temporary solution only - as a fit to experimental data. Exact solution should be a finite combination of trigonometric functions.
Some elements of such a analyse can be found e.g. at [2]. The authors suggested some influence curve for an object in a house. Apart from that they suggest that influences of the houses interfere with each other. They say that similar (but not the same) story is with the influence of signs. However, I have some doubts. First of all, the authors did not write anything about how did they reach their results and did not provide any evidence (estimated after long research and use in practice - it may be different in the original but something like that). Moreover, their curves are continuous but they are not smooth (they have narrow points at the cusps of houses). In addition, they use so-called golden cut which refers to segments, not to angles. Such translation of geometric rules may be dangerous, one should apply them with a great care, as an approximation only. But maybe they are right.
Next question: what happens if a planet (or another object) is in neighbourhood of one of the poles? I think that the further from the equator the weaker is the house's influence - e.g. proportional to cos^2 b where b is the distance from the equator. In other words, the influence would be the strongest on the great circle drawn through the East, Zenith, West and Nadir and it would be the weakest (zero) at the poles or exactly in the North and South. I think similar story would be with the signs - it would decrease with the ecliptic latitude. But why? Because if we take an object in one of the ecliptic poles its ecliptic longitude is not defined so it does not belong to any sign. After an infinitesimal shift (e.g. 0.01") it would be in one of the signs (or between two of them). It seems to be sensible that in such case the influence of the signs should be minimal - in other case there would be discontinuities (or even singularities) on both poles.
Such a system of houses could be suitable even for the sub-polar zones. But what would happen in case that somebody is born exactly at a geographic pole? Or 0.01 mm from a pole? I assume that we can know poles positions with so big precision (it is not true: the error is in order of 1 m). All meridians pass through poles so we cannot speak about the south direction because, in fact, any direction is south - and what about the MC determination? So influence of houses should depend on the geographic latitude (no influence at all at both poles ???!). By the way, it would be quite easy to verify: take two sets of people from near the equator (e.g. India) and a pole (e.g. Norway). If I am right the houses influence on planets for people from Norway should be much smaller.
One can ask Well, but how to understand decreasing influence of the signs and houses?. It is a very good question (next question, please). I suppose that objects near ecliptic poles would be more pure, less influenced by the sign's influence [it would not apply to the planets, e.g. Pluto's maximal distance from the ecliptic is about 17° , for other planets even less, so it would be difficult to catch such tiny effects] and for houses the effect would be that the planet (or other object) would have less influence to things governed by the house.
Of course, at the Southern hemisphere it would be opposite - there MC would be in the north; for the equator (in the tropical region, more precisely) MC would be near the Zenith. Next question: maybe MC is simply the ecliptic longitude of the zenith? Hmm, in such case MC would be exactly between Asc. and Dsc. so we would get equal houses 30° from Asc. and the local meridian would not play any role.
In both methods we have two big peaks near Asc and MC (about 12 points) and two lower peaks near Dsc and IC (about 6 points), between them functions fall to zero. As we want to approximate that by smooth functions the best solution may be trigonomethric ones. Let us take as the first approximation
9/2 [cos (4 alpha) + 1] .
It is not a very good solution - we obtain four equal peaks 9 points each. So let us multiply that by the function that has a maximum between Asc and MC, a minimum between Dsc and IC and in the maximum is 2 times greater than in the minimum. Moreover, its mean value should be 1. Such function may be e.g.. 1/3 [3 + cos (alpha + 45°)] so we obtain the following function:
3/2 [cos (4 alpha) + 1] * [3 + cos (alpha + 45°)]
and it is also shown at Fig. 3 (green line). As we can see, it is a quite good approximation.
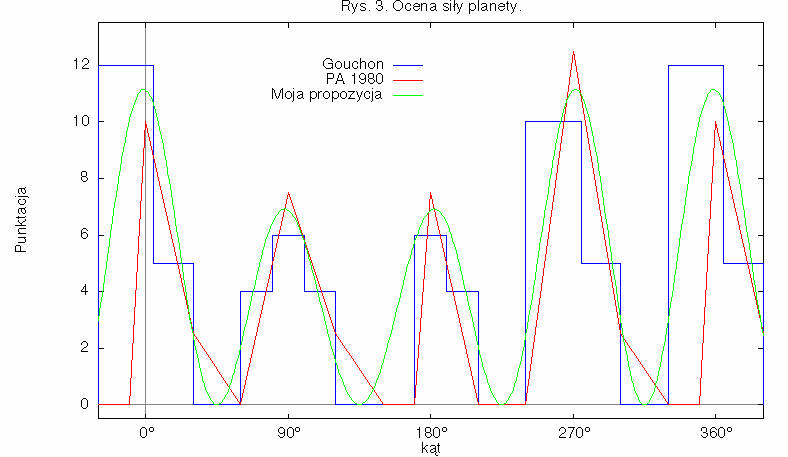
The price for this approximation is some shift of peaks: due to additional factor peaks are not perfectly symmetric and are not placed exactly on the Asc, Dsc, MC and IC. But I think it may be O.K. as the first approximation.